All aboard!
This part will cover
- Forks and Atops
- The tack functions
- Reduce function
Before starting this section, we briefly introduce the commonly used monadic reduce / operator, which applies its left function argument between every element of a vector. More on this in Chapter 4.
⍳10
1 2 3 4 5 6 7 8 9 10
+/⍳10
55
1+2+3+4+5+6+7+8+9+10
55
-/⍳10
¯5
1-2-3-4-5-6-7-8-9-10
¯5
∧/⍳20 ⍝ LCM of numbers from 1 to 20
2520
Some other important functions are the dyadic right and left identity/“tack” functions which return their right or left arguments. They "point" towards which argument they return.
"True"⊣"False"
True
"True"⊢"False"
False
At this point, all the functions we've defined have explicitly referred to the left ⍺ and right ⍵ arguments, for example in the following function range which takes the difference of the largest and smallest values of a vector
5 ⌈ 6
6
5 ⌈ 6 ⌈ 7 ⌈ 8
8
⍝ Maximum between whole vector
⌈/ 5 6 7 8
8
range ← {(⌈/⍵)-(⌊/⍵)}
range 80 49 56 60 100 99 23 19 24 4 50 7
50
or in the following function which takes the (weighted) average of a vector
+/ 1 10 100
111
⍝ Average
(+/ 1 10 100) ÷ 3
37
avg ← {(+/⍵)÷⍴⍵}
avg 1 10 100
37
⍝ Weighing the average by 1 1 1
(+/ 1 10 100 × 1 1 1) ÷ (+/ 1 1 1)
37
⍝ Weighing the average by 2 3 4
(+/ 1 10 100 × 2 3 4) ÷ (+/ 2 3 4)
48
weighted_avg ← {+/(⍺×⍵)÷(+/⍺)}
2 3 4 weighted_avg 1 10 100
48
also in the "plus or minus" function and rounded (or floored) division function
plusminus ← {(⍺-⍵),⍺,⍺+⍵}
5.7 plusminus 0.5
5.05 5.7 6.35
round_div ← {⌊0.5+⍺÷⍵}
1 round_div 3
0
2 round_div 3
1
floor_div ← {⌊⍺÷⍵}
2 floor_div 3
0
4 floor_div 3
1
All of these functions can instead be expressed in terms of special combinations of functions, without referring to the arguments ⍺ and ⍵ at all! Just like magic, it takes some time to learn, but once you do it reveals a rich world of programming spells.
This style of programming is called tacit or "point-free" programming, borrowed from mathematics where it means taking data described using points to be more fundamental than the points themselves, avoiding the need to refer to points explicitly. In this case, taking functions to be more fundamental than their description in terms of explicit arguments. These point-free functions are called trains.
There are two fundamental types of trains which can be created by stringing functions together, more advanced trains will be covered in Chapter 6. The most basic train is the 2-train (fg), in operator form f⍤g, called an atop. The atop evaluates the function f on the result of g applied to the arguments of the train.
The following image shows three equivalent forms of the atop, the first being the APL syntax for the atop, the second being a tree-like representation of the atop where the evaluation happens from bottom to top, and the third is the atop in traditional mathematical notation.
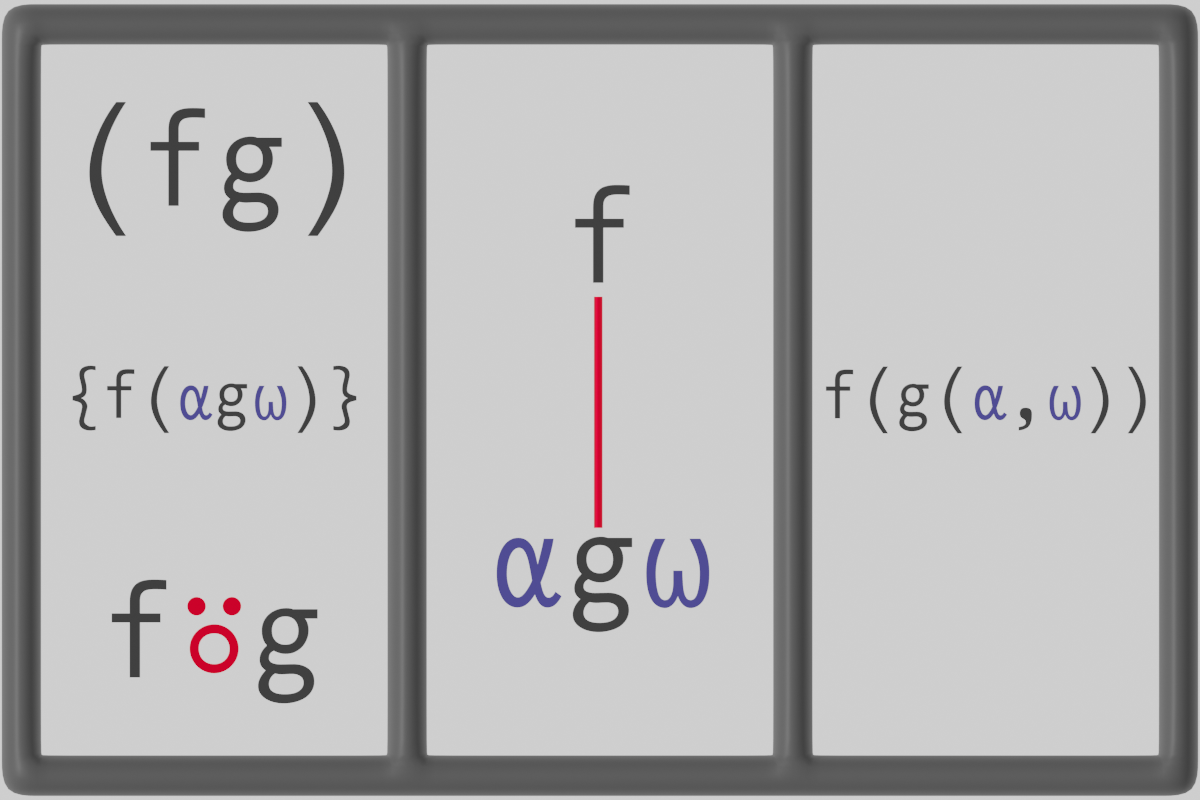
Floored division can be conveniently expressed as an atop.
12÷5
2.4
⌊2.4
2
12(⌊÷)5
2
The second fundamental type of train is the 3-train (fgh), called a fork.

When acting on arguments ⍺ and ⍵, it applies g dyadically to ⍺f⍵ and ⍺h⍵.
The motivation for this specific definition is to match with mathematics, where it is possible to write f+g to get the sum of the values of the functions f and g.
Train trees
The ]Box user command controls how trains are displayed, it is beneficial to set -trains=tree to see a tree-like representation of trains.
f ← {...}
g ← {...}
f+g
f+g
]Box ON
Was OFF
]Box -trains=tree
Was -trains=box
f+g
┌─┼─┐
f + g
Forks here look like forks! The trees are read from bottom up, if there are only two functions at the end of a branch, the result of the right function is applied to the left function, if there are three functions, the middle function is applied to the result of the right and left functions. The values then go up the tree until it reaches the root, at which point it is returned.
Most of the above functions can be expressed as combinations of forks and atops, let's take a look at a few important cases.
The range function is the most straightforward example, it can be written as a single fork
range ← {(⌈/⍵)-(⌊/⍵)}
⍝ is equivalent to
range ← ⌈/-⌊/
range
┌─┼─┐
/ - /
┌─┘ ┌─┘
⌈ ⌊
The functions f and h here are the maximum ⌈/ and the minumum ⌊/, with g being the difference -. When only given a right argument, the above range function evaluates the maximum ⌈/⍵ and the minimum ⌊/⍵, then takes the difference - between them, as is intended.
An example of a fork over a fork is the plusminus function,
plusminus ← {(⍺-⍵),⍺,⍺+⍵}
⍝ is equivalent to
plusminus ← -,⊣,+
⍝ or with redundant parentheses -,(⊣,+)
plusminus
┌─┼───┐
- , ┌─┼─┐
⊣ , +
From the tree representation of plusminus, it is first seen that the function evaluates ⊣ and + to the arguments ⍺ and ⍵, then applies , between them. The result is then applied to the , above, with the result of -. The result is (⍺-⍵),((⍺⊣⍵),(⍺+⍵)) which is exactly (⍺-⍵),⍺,⍺+⍵.
The reason plusminus is interpreted as a fork over a fork is that APL function evaluation is always read from right to left. This extends to longer trains where, for example, (f g h i j k) is interpreted as (f (g h (i j k))), an atop over a fork over a fork.
The rounded division function can be written as an atop over an atop,
round_div ← {⌊0.5+⍺÷⍵}
⍝ is expected to be equivalent to
⌊((0.5+)÷)
SYNTAX ERROR: Missing right argument
⌊((0.5+)÷)
∧
What's going on here? The reason this doesn't work is that ⌊((0.5+)÷) is not purely composed of functions, it contains a value 0.5 and thus is not interpreted as a train. One way around this is to write ⌊({0.5+⍵}÷), which defeats the purpose of point-free programming. Instead, the bind ∘ function can be used to create a monadic function from a dyadic one. In this case, the dyadic function + is bound to the left argument 0.5 as 0.5∘+, which is now a monadic function equivalent to {0.5+⍵}.
round_div ← {⌊0.5+⍺÷⍵}
⍝ is equivalent to
round_div ← ⌊(0.5∘+÷)
round_div
┌┴─┐
⌊ ┌┴┐
∘ ÷
┌─┴─┐
0.5 +